Back to home page

Research

Cell & cellular bio-physics

The mechanical interactions between a cell and its environment play a dominant role in many biological processes including gene expression and morphogenesis. Furthermore, cellular interactions and collective cell migration are not only critical to tissue regeneration but also key to cancer metastasis and tumor invasion. Although recent conceptual, theoretical and computational advances have provided access to mechanical fields, e.g. forces and displacements, in two-dimensions, the three dimensional fields remain inaccessible

Physics of confined fluids & capillary phase transition

The behavior of bulk fluid contrast significantly with that of a confined fluid. This is a consequence of pore morphology, topology and the strength of fluid-solid interactions that alter the energy landscape of a fluid. The effect of confinement on fluid behavior is of interest for a range of scientific and engineering applications. In the case of disordered porous materials, the effect of underlying effective random fields induced by structural and/or chemical disorder on degree of confinement, nature of phase transition, and critical exponents are still unclear.

Granular physics: Non-convex particle interactions

Considering the large carbon footprint of cement production as building materials, jammed granular structures made from entangled non-convex particles can inspire a new class of building materials. While recent studies have demonstrated the ability of such structures to carry tensile forces, the interplay of particle topology, interlocking capability and mechanical behavior remains to be fully unraveled.

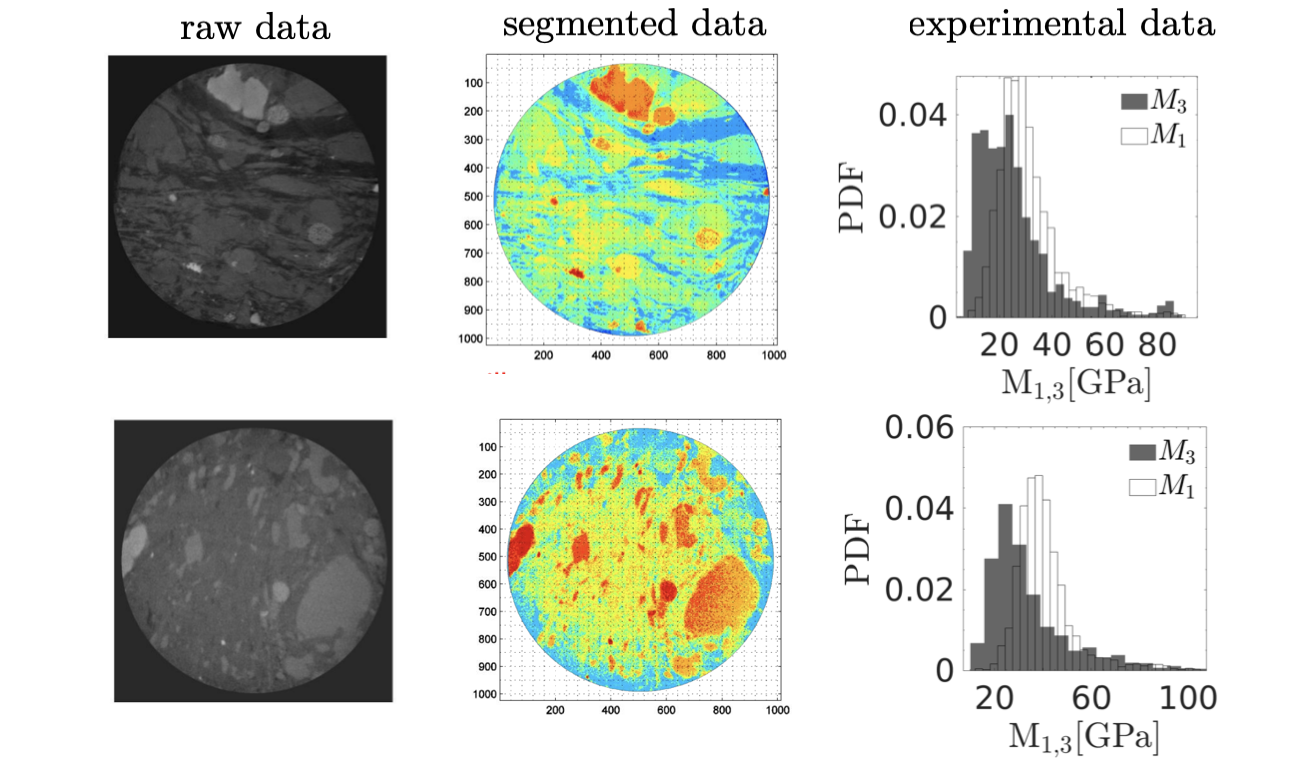
Mechanics & poromechanics of highly heterogeneous solids

Continuum based modeling approaches have limited capabilities to capture the spatial distribution of solid constituents and their mechanical interactions. Primarily built on Eshelby’s inclusion problem and mean-field based homogenization methods, continuum micromechanics approaches reduce the spatial distribution of the solid constituents and their mechanical interactions to effective fields. Furthermore, perturbation based solutions in statistical continuum mechanics are limited to small fluctuations in mechanical properties and thus unable to capture heavy-tailed distributions characteristics of highly heterogeneous media. For these materials with the length scale of observation often on par with that of the inclusions, defining a representative elementary volume that satisfies scale separability - a requirement for any continuum approach - becomes an impractical task. In this vein, we developed a discrete theoretical and computational framework that addresses the limitations encountered in the continuum approach.